1. Koch曲线
瑞典数学家Helge von Koch,在1904年发表的“从初等几何构造的一条没有切线的连续曲线”的论文中提出Korch曲线。它的描述如下:
- 指定一条线段的长度\(l\)(可以理解为第0次迭代)
- 将这条线段三等分,并以中间的线段为底边构造一个等边三角形,然后去掉底边
- 对2中生成的曲线的每一条边重复2的操作(每操作一次称为一次迭代)
最终得到的集合图形长度为:$$L=l*(\frac{4}{3})^{N}$$,其中的N指的是迭代次数。
1.2 绘制方法:
- 如果N=0,直接画出L长的直线即可
- 如果N=1(第一次迭代),画出长度为L/3的线段;画笔向左转60度再画长度为L/3长的线段;画笔向右转120度画长度为L/3长的线段;画笔再向左转60度画出长度为L/3的线段
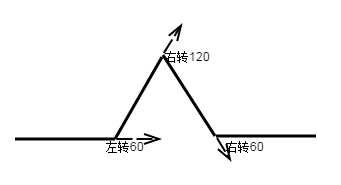
- 如果n>1,第n次迭代相当于:n-1次迭代;画笔左转60度;n-1次迭代;画笔右转120度;n-1次迭代;画笔左转60度;n-1次迭代。
1.3 Python代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| # -*- coding: utf-8 -*-
import turtle
Division = 3.0
DirectionAangle = [('left',60),('right',120),('left',60)]
def call(name):
if name == 'left':
return turtle.left
else:
return turtle.right
def koch(n, length):
if n==0:
turtle.forward(length)
else:
for DA in DirectionAangle:
koch(n-1,length/Division)
call(DA[0])(DA[1])
koch(n-1,length/Division)
koch(n=2, length=100)
turtle.done()
|
1.4 绘制的图形
下面分别是n=3, length=300和n=4, length=400生成的Koch曲线
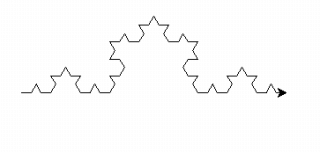
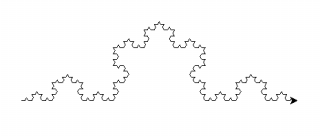
2. Julia集
2.1 绘制方法
在上一篇博文中提到过,点击前往
- 设定初值 p,q, 最大的迭代次数 N, 图形的大小 a,b, 及使用的颜色数 K.这里需要注意的是c的模总是小于2。可以证明当c的模大于2时,进行迭代必将发散到无穷。
- 设定区域的界值 \( M\ge max(2,\sqrt{p^2+q^2}) \)
- 将区域\(R=[-M,M]\times[-M,M]\)分成\(a\times b\)的网格,分别以每个网格点为初值(\(x_0,y_0\))。利用上面替换之后的公式做迭代。如果对\(n \le N\)所有的都有\({x_n}^2+{y_n}^2\le M^2 \),则将象素\((i, j)\)置为这一种颜色。如果从某一步 n 开始\({x_n}^2+{y_n}^2\ge M^2 \),则将象素 \((i, j)\)置为不同颜色。
2.2 Python代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| # -*- coding: utf-8 -*-
import matplotlib.pyplot as plot
import numpy as np
p=0.45 #初始值c的实部
q=-0.1428 #初始值c的虚部
N=800 #最大迭代次数
M=100 #迭代区域的界值
a=3.0 #绘制图的横轴大小
b=3.0 #绘制图的纵轴大小
step=0.005 #绘制点的步长
def iterate(z,N,M):
z=z*z+c
for i in xrange(N):
if abs(z)>M:
return i
z=z*z+c
return N
c=p+q*1j
i=np.arange(-a/2.0,a/2.0,step)
j=np.arange(b/2.0,-b/2.0,-step)
I,J=np.meshgrid(i, j)
ufunc=np.frompyfunc(iterate,3,1)
Z=ufunc(I+1j*J,N,M).astype(np.float)
plot.imshow(Z,extent=(-a/2.0,a/2.0,-b/2,b/2.0))
cb = plot.colorbar(orientation='vertical',shrink=1)
cb.set_label('iteration counts')
plot.show()
|
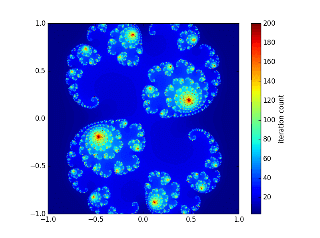
2.3 绘制的图形
参数:p=0.285 q=0.01 N=200 M=100 a=2.0 b=2.0 step=0.005 (左图)
参数:p=0.45 q=-0.1428 N=200 M=100 a=2.0 b=2.0 step=0.005 (右图)
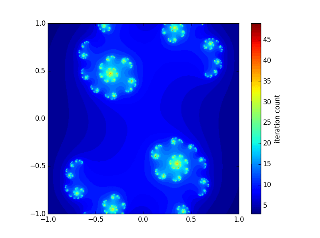
还有其他的初始c值可以绘制出十分漂亮的图案,例如:
c = -0.70176+-0.3842j
c = -0.835+-0.2321j
c = -0.8+0.156j
c = 0.285
3. Mandelbrot集
数学定义:
$$f_c(z) = z^2+c$$
Mandelbrot集是\(f_c(z)\)在z=0,关于复数c=x+yi的函数迭代不发散序列集合。
绘制Mandelbrot集最简单的方法是使用逃逸时间进行绘制。逃逸时间指的是,在指定范围M进行有限次数N迭代,而不超出M区域的次数。使用不同的颜色绘制不同的迭代次数。
- 设置迭代的最多次数,N
- 设置初始化\(z_0\)的值,
- 设置逃逸半径R的值,通常为2
3.1 绘制方法
3.2 Python实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| # -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plot
x0=0 #初始值z0的x0
y0=0 #初始值z0的y0
zoom=1.0 #放大倍率
N=100 #最大迭代次数
R=2 #迭代半径
a=4.0 #绘制图的横轴大小
b=3.0 #绘制图的纵轴大小
step=0.005 #绘制点的步长
def iterate(c,N,R):
z=c
for i in xrange(N):
if abs(z)>R:
return i
z = z*z+c
return N
x=np.arange(-a/(2.0*zoom)+x0,a/(2.0*zoom)+x0,step)
y=np.arange(b/(2.0*zoom)+y0,-b/(2.0*zoom)+y0,-step)
cx,cy=np.meshgrid(x, y)
c = cx + cy*1j
ufunc=np.frompyfunc(iterate,3,1)
Z=ufunc(c,N,R).astype(np.float)
plot.imshow(Z,extent=(-a/2.0,a/2.0,-b/2,b/2.0))
cb = plot.colorbar(orientation='vertical',shrink=1)
cb.set_label('iteration counts')
plot.show()
|
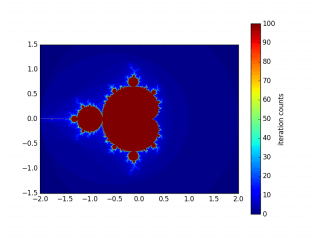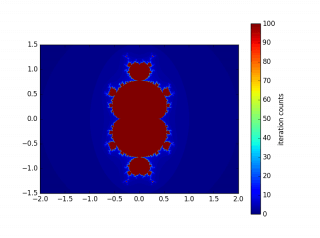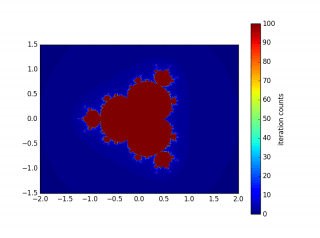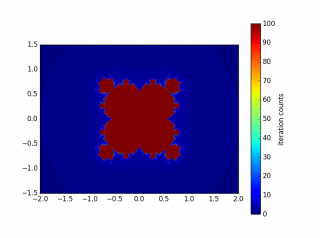
3.3 绘制的图形
图中是使用参数:x0=0 y0=0 zoom=1.0 N=100 R=2 a=4.0 b=3.0 step=0.005。生成的图像。不同的是,它们依次使用的是二次、三次幂的迭代。
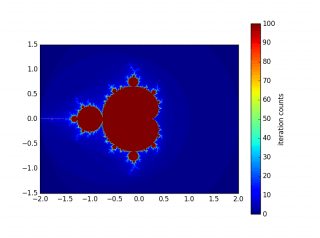
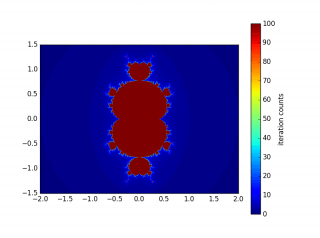
最后,还可以使用ImageMagick工具,将生成的图像制作成一个动态GIF。